Disjoint Set Data Structure

Anonymous included in Algorithm
  

一般并查集

并查集是一种树形的数据结构，用于处理集合的合并和查询问题，支持以下两种操作:

  • 查找（Find）：确定某个元素处于哪个子集
  • 合并（Union）：将两个子集合并成一个集合

一个集合具有以下两点合法性要求：

  1. 放入同一集合中的元素是具有某种共同属性的

    例如维护一棵家族树，所有元素的共同属性是同一家族

  2. 若集合维护的是一种关系，这种关系必须具有传递性

    例如一个集合是不能维护不等关系的，因为$x!=y \ + \ y!=z \ \neq \ x!=z$

需要注意的是以上两点要求并不是非此即彼的关系，某些集合看似是在维护一种关系，但本质上是在维护一个共同属性。例如“相等关系”的维护本质上也是在维护数据的值这种共同属性

初始化

最初状态下，每个节点都属于一个集合

1
2

// N个节点 p[i]: 元素i的父亲元素，p数组含义下同
for (int i = 0; i < N; ++i) p[i] = i;

查找及路径压缩

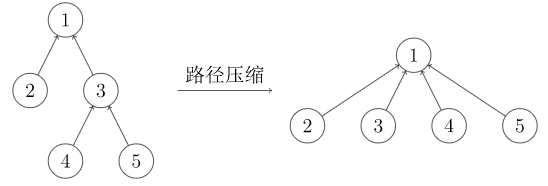
并查集维护的信息是元素所处的集合，即给定一个元素，我们只需要确定其处在哪个集合中。

若从每个集合中各选择一个代表元素，则只需要找到元素所在集合中的代表元素即可。

若将各元素的父亲元素指向代表元素则可快速完成这项操作。

实际效果如下图所示：

https://cdn.jsdelivr.net/gh/G-ghy/cloudImages@master/202201252315685.png

1
2
3
4

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

合并

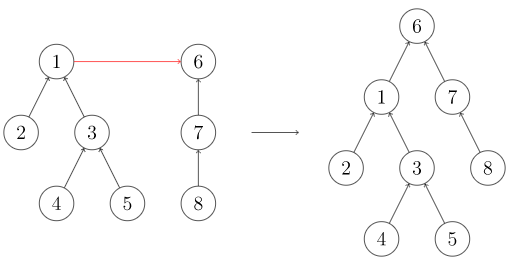
两个集合进行合并，只需令其中一集合代表元素的父亲元素指向另一集合的代表元素。实际效果如下图所示：

https://cdn.jsdelivr.net/gh/G-ghy/cloudImages@master/202201252318311.png

1
2
3
4

// 将元素x所在集合同元素y所在集合进行合并
int px = find(x);
int py = find(y);
p[px] = py;

启发式合并（按秩合并）

目前还没有遇到必须使用启发式合并的题目或知识点，暂时不做探讨。

带权并查集

在一般并查集中，一个集合仅能表示一种关系

带权并查集是指在一般并查集的边上定义某种权值、以及这种权值在路径压缩时产生的运算，从而在一个集合中维护多种关系

每个集合一种关系，多个集合维护多种关系 or 一个集合通过加入边权维护多种关系？

在面对多种关系时，第1种策略具有以下2点问题：

  1. 不同集合之间信息不能互通，因此不同集合之间无法实现传递性
  2. 关系较多时维护较为复杂，有些情况下由于第1点问题的存在关系甚至无法维护

具体的例子暂时还没有遇到

核心思想

保存相对关系

带权并查集需要维护多种关系，实际过程中往往选择维护与集合的代表元素之间的关系，任意两个元素之间的关系通过各自与代表元素的关系综合推导得出

例题分析

为了引申出带扩展域并查集，这里采用奇偶游戏一题对带权并查集的使用流程进行分析

问题描述

https://cdn.jsdelivr.net/gh/G-ghy/cloudImages@master/202201262339414.png

解题思路

奇偶游戏是如何转化为并查集问题的这里不再赘述，简言之，核心问题是判断两元素奇偶性是否相同

显然，这里需要维护两种关系，1.具有相同奇偶性 2.具有不同奇偶性

在一般并查集的合法性条件中有提到传递性这一问题，“不同奇偶性”这一关系同“不等关系”，是不具备传递性的，因此无法采用两个集合分别维护两种关系，因此考虑带权并查集并做出以下规定

d[i]: 在并查集中元素i距离代表元素的距离 d[i] = 0： 元素i与代表元素具有相同奇偶性 d[i] = 1: 元素i与代表元素具有不同奇偶性

通过距离d确定元素关系

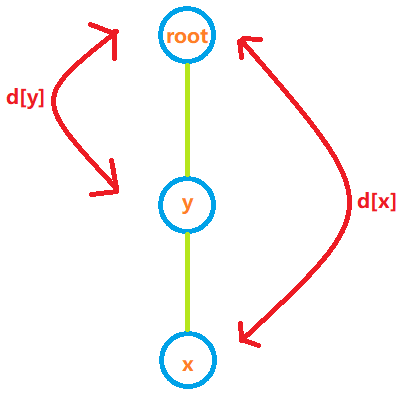
https://cdn.jsdelivr.net/gh/G-ghy/cloudImages@master/202201262356896.png

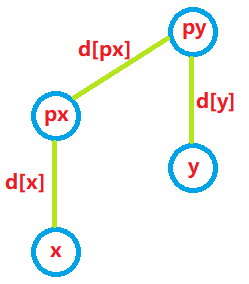
假设有两个元素x和y，两者处于同一集合之中，形式如上图所示

x与y的奇偶性关系应当由x与y之间的距离决定，即(d[x] - d[y] + 2) % 2。

对于以上计算方法，做出以下几点说明：

  1. 模2的原因在于这里所说的距离并非物理距离，而是逻辑距离，是模2意义下的
  2. d[x] 与 d[y] 减法的顺序并不重要，这里寻求的只是一种相对距离
  3. 加2的原因在于我们无法确定d[x] 和 d[y]的大小关系，先加2再模2，使得结果恢复到非负数范围内同时保证相对关系结果的正确性便于判断

路径压缩时距离d的维护方法

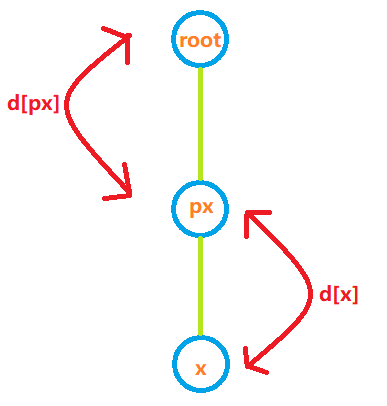
https://cdn.jsdelivr.net/gh/G-ghy/cloudImages@master/202201270008054.png

find()在寻找root代表元素时会进行递归操作，在px没有被修改为root之前，d[px]已正确完成更新，d[x]仍然保留着x与px间的距离

因此，x与root间的距离应当为(d[x] + d[px]) % 2

对于该计算方法的说明见上，不再赘述

1
2
3
4
5
6
7
8

int find(int x) {
    if (p[x] != x) {
        int root = find(p[x]); // 注意讲解中提到的“在px没有被修改为root之前”这一条件
        d[x] = (d[x] + d[p[x]]) % 2;
        p[x] = root;
    }
    return p[x];
}

合并时距离d的维护方法

需要说明的是，不同题目这里的计算方法并不相同，不需要记忆公式，只需要保证合并后两元素之间的关系能够得以正确计算获取即可

https://cdn.jsdelivr.net/gh/G-ghy/cloudImages@master/202201272319417.png

对于本题，合并时包含以下两种情况。

为了描述的方便，设两个元素为x和y，且合并是将x分支合并到y分支上

  1. 两元素奇偶性相同

两元素奇偶性相同对应到距离d上的表现为：(d[y] - d[x] + 2) % 2 == 0

因此，合并后的距离要求为：(d[y] - (d[x] + d[px]) + 2) % 2 == 0

可以解得，d[px] = (d[y] - d[x] + 2) % 2

  1. 两元素奇偶性不同

两元素奇偶性相同对应到距离d上的表现为：(d[y] - d[x] + 2) % 2 == 1

因此，合并后的距离要求为：(d[y] - (d[x] + d[px]) + 2) % 2 == 1

可以解得，d[px] = (d[y] - d[x] + 1 + 2) % 2

解题代码

点击查看代码
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82

#include <cstring>
#include <cstdio>
#include <cmath>
#include <iostream>
#include<string>
#include <algorithm>
#include <vector>
#include <queue>
#include <deque>
#include <stack>
#include <set>
#include <map>
#include <unordered_map>
#include <unordered_set>

using namespace std;

constexpr int N = 10010;
constexpr int INF = 0x3f3f3f3f;

int n, m;
int p[N], d[N];
unordered_map<int, int> s;

// 离散化
inline int get(int x) {
    if (!s.count(x)) s[x] = ++n;
    return s[x];
}
int find(int x) {
    if (p[x] != x) {
        int root = find(p[x]);
        d[x] = (d[x] + d[p[x]]) % 2;
        p[x] = root;
    }
    return p[x];
}
void solve() {
    cin >> n >> m;
    n = 0; // 离散化仍然使用n作为点数,所以此处初始为0

    for (int i = 0; i < N; ++i) p[i] = i;

    int res = m; // 若不存在非法条件则答案为m
    for (int i = 1; i <= m; ++i) {
        int l, r;
        string type;
        cin >> l >> r >> type;
        l = get(l - 1), r = get(r);
        int pl = find(l), pr = find(r);

        if (type == "even") { // 相同奇偶性，如果并查集中pl != pr则一定不会发生矛盾，添加相同关系即可；若pl == pr, 需要查看并查集中保存的关系是否与此时给定的条件矛盾
            if (pl != pr) {
                p[pl] = pr;
                d[pl] = (d[r] - d[l] + 2) % 2; // 两元素具有相同奇偶性时的合并方法
            } else {
                if ((d[r] - d[l] + 2) % 2 == 1) { // 并查集中维护的是l和r具有不同奇偶性，与此时条件矛盾
                    res = i - 1;
                    break;
                }
            }
        } else { // 不同奇偶性
            if (pl != pr) {
                p[pl] = pr;
                d[pl] = (d[r] - d[l] + 1 + 2) % 2; // 两元素具有不同奇偶性时的合并方法
            } else {
                if ((d[r] - d[l] + 2) % 2 == 0) { // 并查集中维护的是l和r具有不同奇偶性，与此时条件矛盾
                    res = i - 1;
                    break;
                }
            }
        }
    }

    cout << res << '\n';
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    solve();
    return 0;
}

带扩展域并查集

假设元素有n种可能，则开启n个并查集，每一个并查集维护一种可能取值，从而包含所有情况，是一种枚举的思想

这样做是可以维护传递关系的，能否传递关系关键在于一条关系链是否处在一个并查集中，如果关系链跨越多个并查集则无法传递

维护哪些条件之间可以相互推导

目前的核心问题是如何才能理解扩展出来的域的含义

还有就是在不同的题目中如何理解带扩展域并查集维护的是关系，或者说条件

在食物链一题中，是包含3个种群的，A，B，C，

仅仅在说x吃y时，x有可能是A种群，也可能是B种群，也可能是C种群

所以用x表示属于A种群，x+n表示属于B种群，x+2n表示属于c种群

但是这样规定那个条件就不是很好理解

Updated on 2024-11-14 
Back | Home
0%