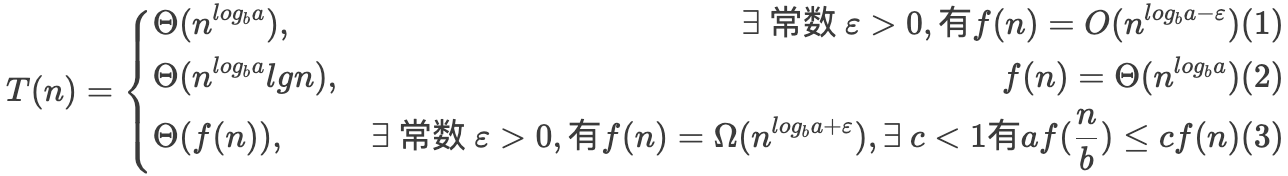Divide and Conquer Algorithm
4 种递归式求解方法
代入法
猜测一个界,然后用数学归纳法证明这个界是正确的。
- 猜测解的形式
- 用数学归纳法求出解中的常数,并证明解是正确的
猜测解这个难度还是比较大的,所以从题目的角度来说,一般会设直接给出解,要求证明,例如下题
证明: $T(n) =2T(\lfloor \frac{n}{2} \rfloor + 17) + n$ 的解为 $O(nlgn)$
所以说,代入法更侧重是一种证明方法,而非求解方法
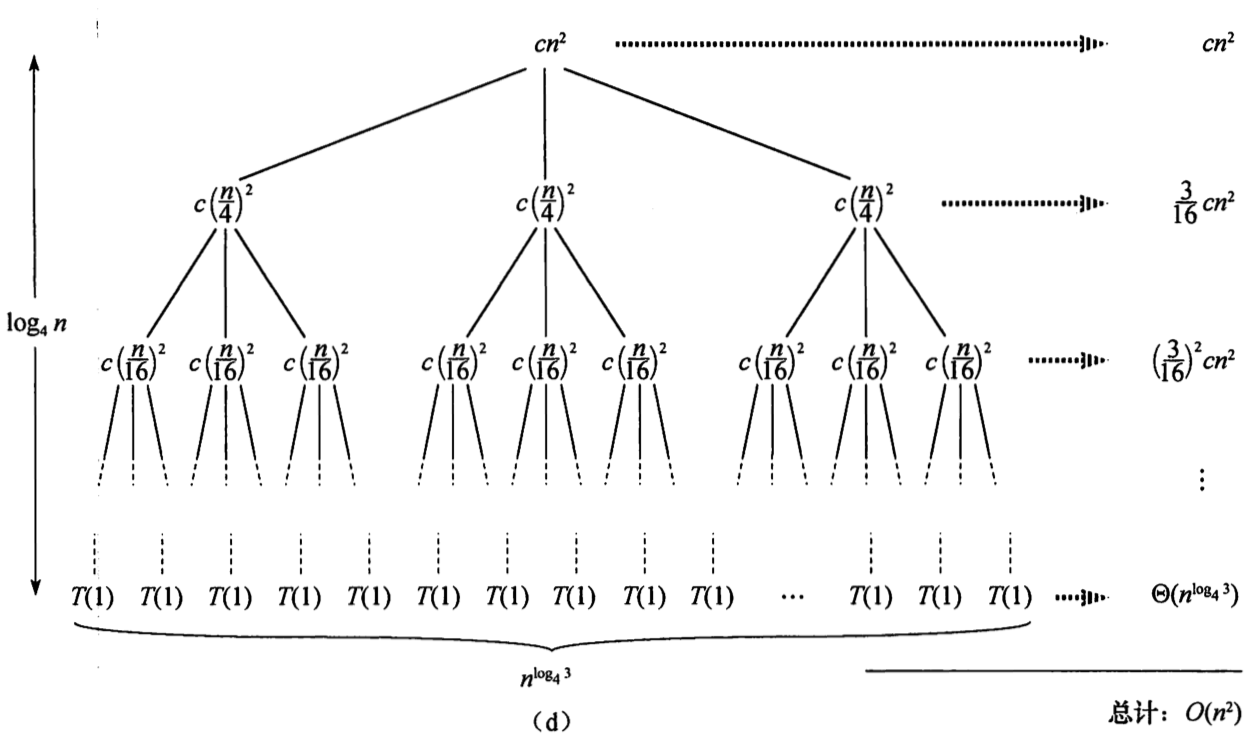
递归树法
将递归式转换为一棵树,其结点表示不同层次的递归调用产生的代价。然后采用边界和技术来求解递归式。
迭代法
本质上来说,迭代法可以看为一种特殊的递归树形式,求解过程并不会把树画出来,而是直接在公式推导中进行计算
主定理
求解形如 $T(n) = aT(\frac{n}{b}) + f(n)$ 的递归式的界
在给出它的计算方法之前,首先对这一递归式的含义进行简要介绍: 规模为 n 的问题分解为 a 个子问题, 每个子问题规模为 $\frac{n}{b}$, 其中 a 和 b 都是正常数。 a 个子问题递归地进行求解,每个花费时间 $T(\frac{n}{b})$ 。函数 f(n) 包含了问题分解和子间题解合并的代价。
主定理:
$$ T(n) = \left{ \begin{align} & \Theta(n^{log_ba}), & \exists \ 常数 \ \varepsilon > 0, 有f(n) = O(n^{log_ba - \varepsilon}) \ & \Theta(n^{log_ba}lgn), & f(n) = \Theta(n^{log_ba}) \ & \Theta(f(n)), & \exists \ 常数 \ \varepsilon > 0, 有f(n) = \Omega(n^{log_ba + \varepsilon}), \exists \ c < 1 有 af(\frac{n}{b}) \le cf(n) \end{align} \right. $$
从上述内容不难看出,$f(n)$ 和 $n^{log_ba}$中的较大者决定了递归式的值。上述公式从上至下依次表示$f(n)$ <, =, > 三种情况
不同方法常用适用类型
使用代入法,则递归式一般是包含难以手工计算的因素,直接计算相对困难。 e.g. $T(n) =2T(\lfloor \frac{n}{2} \rfloor + 17) + n$。携带下取整,这很难通过人工计算求解出一个具有固定形式的解
使用递归树,则递归式一般是会分出多个分支,一方面不适用于主定理,另一方面迭代法不便处理多个分支,因此通过树形来处理这种多分支。e.g. $T(n) = T(\frac{n}{2}) + T(\frac{n}{4}) + cn$
使用迭代法,则递归式中子问题的规模一般呈常数量级减小,且不存在多个分支。e.g. $T(n) = T(n - 1) + \frac{1}{n}$
使用主定理,则递归式中子问题的规模一般呈倍数量级减小,且不存在多个分支。e.g. $T(n) = 2T(\frac{n}{2}) + n^2logn$
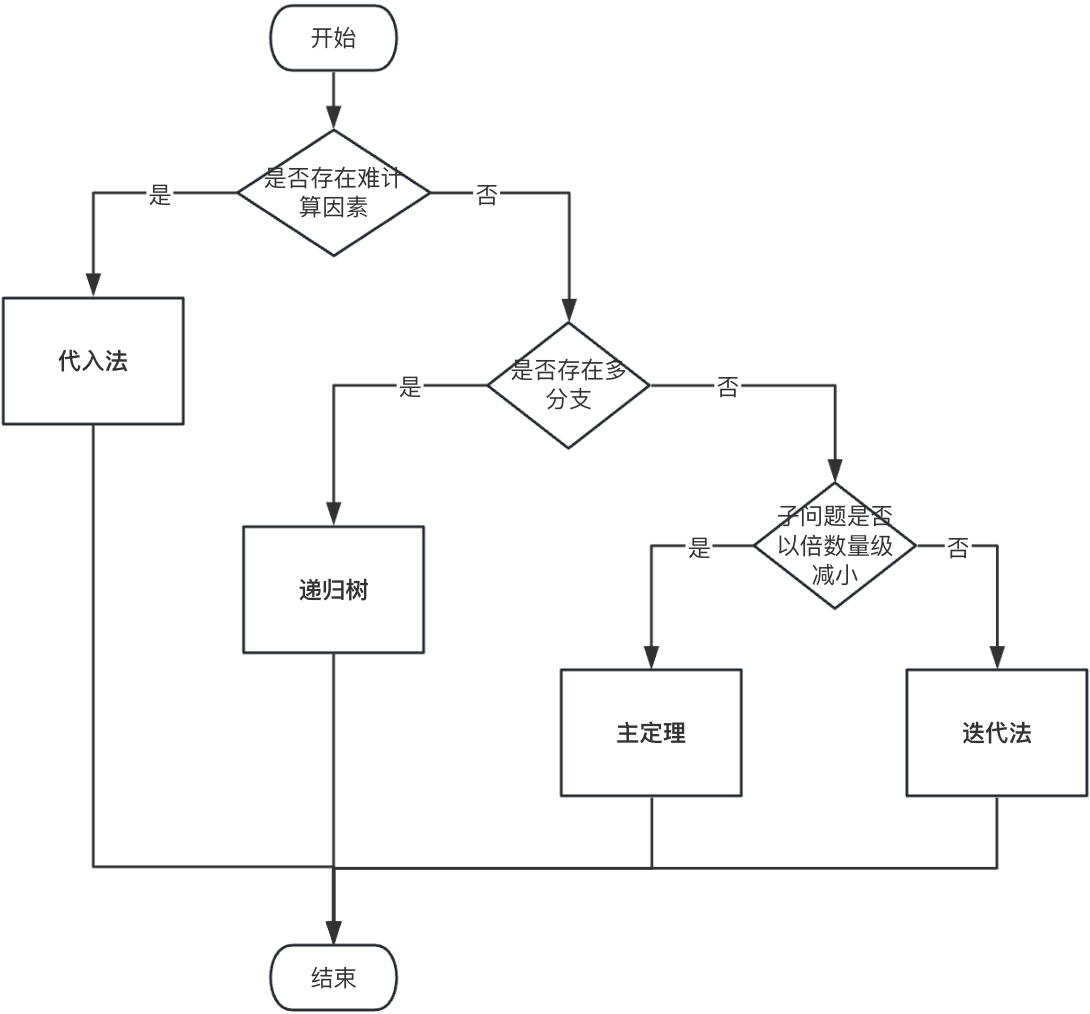
对于方法的选择,总结如下