NP Completeness -

Anonymous included in Algorithm

2023-11-26 2024-05-18

Contents

NP完全性的核心逻辑

NP完全问题是为了反映一个问题有多难，而不是为了反应它有多简单

有多项式时间算法的问题称为易解的，不存在多项式时间算法的问题成为难解的（这里的多项式时间算法包含确定型图灵机多项式时间算法，也包含非确定性图灵机多项式算法）

性质

问题的分类

最优化问题(optimization problem)
判定问题(decision problem) 两类问题的关联在于：通常，通过对待优化的值强加一个界，就可以将一个给定的最优化问题转化为一个相关的判定问题了。同时从直观上来看，如果最优化问题容易，则对应的判定问题也是容易的。换言之，如果我们能够证明判定问题是困难的，则相当于也说明了对应的最优化问题是困难的.

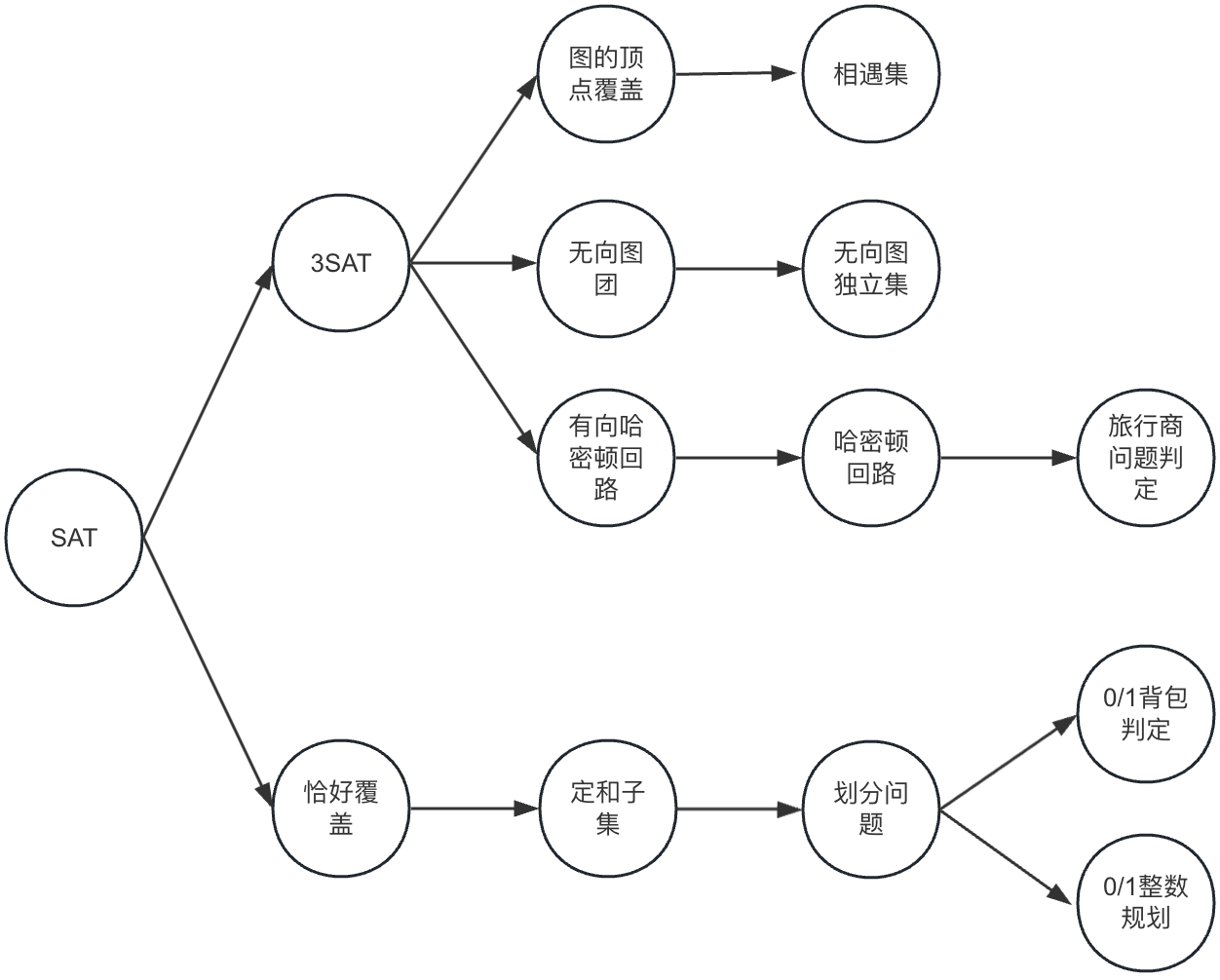
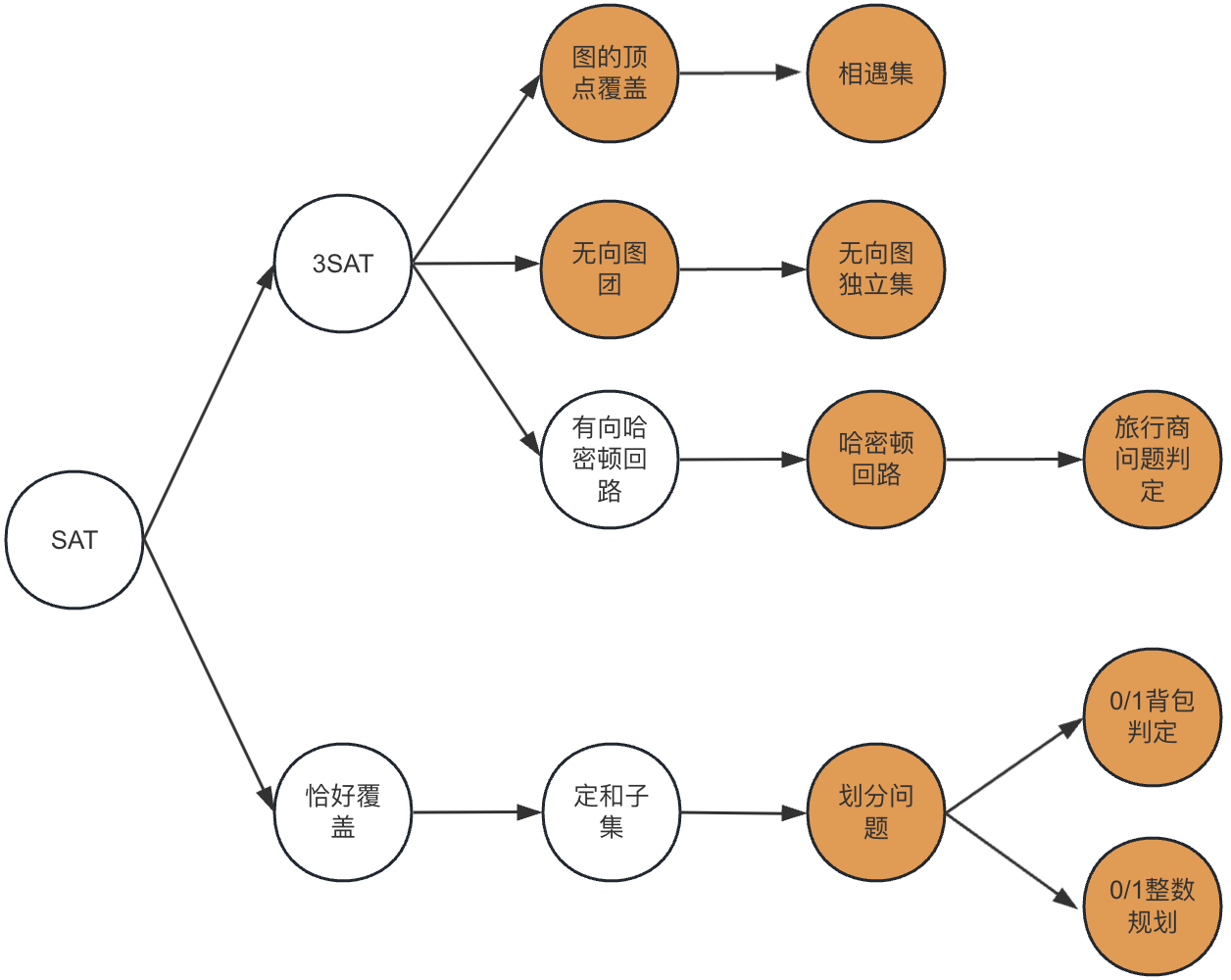
NPC问题

相关问题描述

问题描述三部曲：1.有什么 2.找什么 3.目的是什么

顶点覆盖

存在一个顶点集包含所有边中的至少一个顶点

V, E, k, 找V'

给定图G=(V, E), 正整数$K \le \left| V \right|$
是否存在V的一个子集V’, $\left| V’ \right| \le K$
s.t. V’包含图G任何一条边中至少一个顶点

相遇集

存在一个集合的子集包含原集合的子集族中每一个子集中的至少一个元素

S, C, K, 找S'

给定集合S, S的子集族C, 正胜数$K \le \left| S \right|$
是否存在S的一个子集S’, $\left| S’ \right| \le K$
s.t. S’与C中任何一个子集的交集非空

划分问题

集合划分成两部分，两部分元素的权值和相等

01整数规划问题

关键是记住 $$ Ax \le b \ C^Tx \ge D $$

独立集 / 团

无需记忆问题描述，只需要知道独立集和团都是点集。

独立集这个点集中，任意两个顶点均不相邻
团这个点集中，任意两个顶点均相邻

补图和原图的顶点没变，补图中两个顶点之间有边（相邻）当且仅当原图中这两个顶点之间没边（不相邻）

哈密顿回路问题

给定图G=(V, E)
是否存在节点的一个排列
s.t. 存在包含全部节点的一条回路

旅行商判定问题

给定一个城市集合C, 每对城市之间的距离d，正整数D
是否存在一个C中城市的排列
s.t. 排列形成一个回路，距离和$\le D$

0/1背包判定问题

总容量不超过某值情况下，总价值能否超过一个值

NPH问题

旅行商问题（TSP）
0/1背包问题

为什么如何重视判定问题？ 无论是何种问题，关于P,NP,NPC,NPH都是在考虑如何描述解决问题的难易程度，这是这一章的核心逻辑最优化问题或者说搜索问题，都可以比较简单的对应到一个判定问题，因此最优化问题易解->判定问题易解，逆反命题自然成立。而这种所谓的对应，专业的描述就是多项式时间变换，或者说属于归约操作

关于这一内容，出自《算法设计与分析（第2版）》屈老师的那一本书，由最优化问题->对应的判定问题是最开始讲述这类问题时进行的一种操作，这个准确来说叫做归约。而多项式时间变化是证明NPC或者NPH时的说法，不过多项式时间变换也是归约的一种

简单来说，判定问题的定义是明确且易表达易理解的，同时最优化问题是容易转换为判定问题的。

不过有一个疑问是为何只考虑最优化问题，在课程中提及的问题都是最优化问题，而是书籍中给出的示例一般也是最优化问题，但是一半问题中并非仅仅是最优化问题，不过似乎都是易转换为判定问题的

计算复杂度

两个重要工作：

确定问题计算复杂度的一个上界
确定问题计算复杂度的一个下界
以比较为基础的检索问题的时间下界$\Omega(logn)$
以比较为基础的排序问题时间下界$\Omega(nlogn)$
找最大值时间下界$\Omega(n-1)$
找最大值和最小值时间下界$\Omega(\lceil \frac{3n}{2} \rceil - 2)$ (分治)
找次大值时间下界$\Omega(n + \lceil logn \rceil - 2)$ （锦标赛算法，首先找最大值下界为$n - 1$，树形结构中在输于最大值的元素中找次大值时间下界$\lceil logn \rceil - 1$）
找中位数时间下界$\Omega(\frac{3n}{2} - \frac{3}{2})$
找第k小值时间下界$\Omega(n + min(k, n - k +1) - 2)$

证明

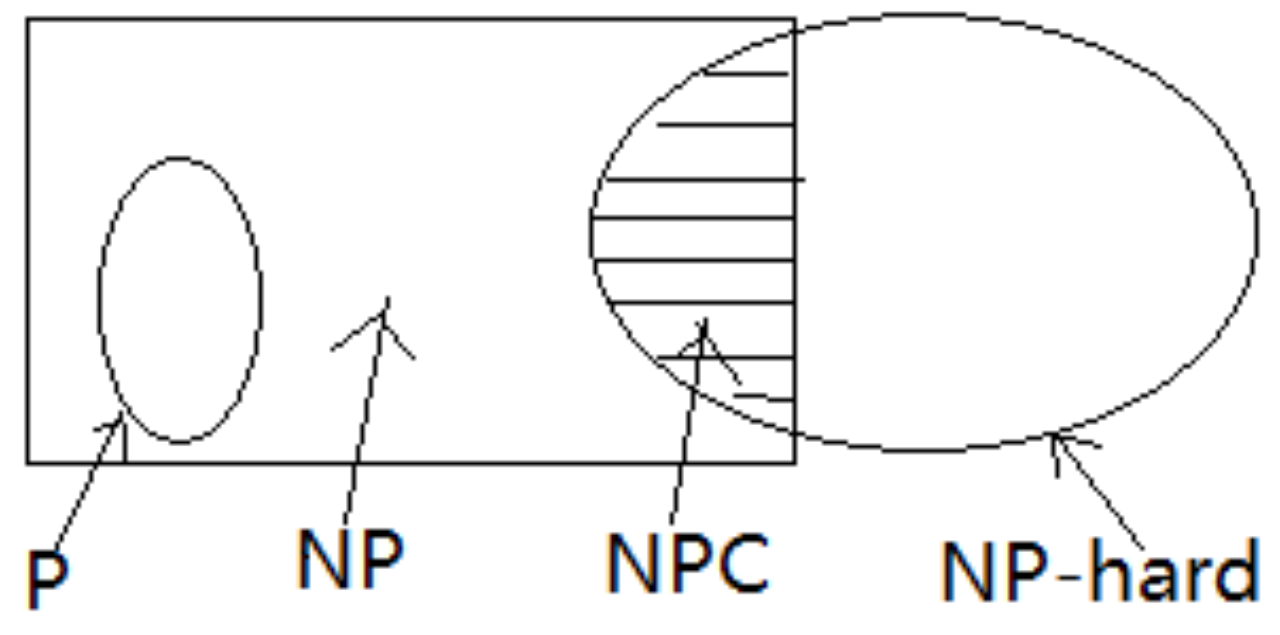
所有多项式时间内可验证的问题组成了NP类问题，其中能够在多项式时间内求解的为P类问题，能够由其他NPC问题归约得到的是NPC问题

P : 多项式时间内可求解，存在确定型多项式时间算法

NP：多项式时间内可验证，存在非确定型多项式时间算法（随便猜一种情况然后验证，把所有情况猜完一定可以找到解）

证明问题是NP的，根本上来说就是判断是否存在一种非确定型多项式时间算法能够求解出答案，对于这种算法的描述可以用猜想和验证两个阶段来表述。而这种算法是多项式时间的等价于猜想和验证环节都是多项式时间的，而且猜想和验证都只是需要考虑一个实例要如何处理。如果说总共需要猜想和验证的实例数是指数级($2^n$)，但是一个实例的猜想和验证都只是需要多项式时间，那么这种算法依然是多项式时间的，因为非确定型多项式时间算法是跑在NDTM非确定型图灵机上的，是可以并行的。举一个验证阶段无法在多项式时间内完成的例子，旅行商问题，对于旅行商问题的一个实例（注意是旅行商问题，不是旅行商的判定问题），验证环节需要和其他所有回路进行比较，而其他回路数量是指数级的，所以验证环节是无法在多项式时间内完成的（如果是旅行商的判定问题，验证环节是可以在多项式时间内完成的）。

NPC: 首先需要是NP，然后找到另一种NPC问题可以转化到当前问题

为什么需要保证是NP？因为如果当前问题可以从另外一种NPC多项式时间内变换得到，只能说明当前问题不比那个NPC问题简单，有两种可能：1.NPC，2.非NPC的NPH，只有当时NP时才能保证是前者而非后者

给出已知NPC问题实例
给出待证明问题示例
说明最优化问题的原问题是NP的(存在一种多项式时间内猜想和多项式时间的验证方法可以得到问题的解，即存在非确定型多项式时间算法，其中非确定型是指需要猜想这个环节)
说明从一个已知的 NPC 问题的判定问题可以多项式时间归约到原问题的判定问题

4.1 构造一个待证明问题的示例

4.2 假设前一个问题可取得解，证明后一个问题同样存在解

4.3 假设后一个问题可取得解，证明前一个问题同样存在解

4.4 说明一下变换可以在多项式时间内完成

NPH: 首先判断是否为NP问题，如果是NP问题同时还是NPH问题那就只能是NPC问题，如果不是NP问题那就是非NPC的NPH问题，需要保证任意一个NP能够转化到当前问题(显然这是困难的，需要用到NPC的定义来实现)

说明问题不是NP的（验证环节无法在多项式时间内完成）
说明问题的难度不低于NPC

第2步的具体方法目前考虑到的可能有2种：
原问题的判定问题是NPC的，则说明原问题难度不低于NPC
存在一个已知的NPC问题可以多项式时间变换到当前问题

如何解决 NPC 问题

如果实际输入数据规模较小，则指数级运行时间的算法可解决问题
对于一些能在多项式时间内解决的特殊情况，可以单独求解
寻找一些能够在多项式时间内得到近似最优解

证明问题是 NPC 问题的关键步骤

判定问题与最优化问题 NP 完全性不适合直接应用于最优化问题，但适合应用于判定问题

关于这一点最直观的理解方式就是看NPC问题的证明

假设现在要证明一个最优化问题是NPC的，那么第1步中会证明该问题是NP的，此时存在一种非确定型多项式时间算法可以在多项式时间内完成猜想，以及多项式时间内完成验证，从而确定猜想到的解是不是一个合法解。在这一步中，无论是算法还是验证过程，都像是在处理原问题的判定问题。但是不要忽略了，只要我们可以在多项式时间内验证一个解，那么只要所有可能猜到的解中包含最终答案，理论上我们就可以得到这个最终答案并且完成验证过程，这个时候原问题就已经得到解了，那这种猜想验证的算法实际就已经解决了原问题。（回过头来看，在这一部分最后一般会添加一句话“能猜到一个xxx当且仅当yyy中存在一个xxx“，这句话并不是废话，它保证了这种算法在理论上是可以在所有可能的情况中找到一个解的）

第2步会去证明是一个NPC问题，这里证明的并不是原问题那个最优化问题，而是最优化问题对应的判定问题，最后通过判定问题和原问题的难度关系，由于判定问题是NPC，那么原问题是不比NPC简单的问题，结合上述是NP问题，就能够说明是NPC问题了。

根据上述分析，虽然我们要证明的是最优化问题是NPC问题，但是完全可以看为要证明的是最优化问题的判定问题是NPC问题。因为第2步证明的确实就是判定问题是NPC问题，第1步给出的算法本身也是判定问题的形式（判定问题的形式，但是结合上猜想可以解决最优化问题本身）。所以只需要关注判定问题是什么即可。

归约

a.实例的概念: 实例是指某一特定问题的输入

b.多项式时间归约算法：一个多项式归约算法可以在多项式时间内，将A的任何实例a转化为B的实例b，a和b是相同(a为“是”时，b也为“是”)

c.多项式时间归约的目的：A 和 B 之间的 ”易求解性“ 或 ”难求解性“ 是相同的，可通过一个问题的性质推导另一个问题的性质

第一个 NPC 问题