Matrix Multiplication

1. GEMM（General Matrix Multiplication）-通用矩阵乘
2. BLAS (Basic Linear Algebra Subprograms) - 基本线性代数子程序
3. SGEMM (Single precision General Matrix Multiply) - 单精度矩阵乘法
4. DGEMM (Double precision General Matrix Multiply) - 双精度矩阵乘法
5. CGEMM (Complex single precision General Matrix Multiply) - 单精度复数矩阵乘法
6. ZGEMM (Complex double precision General Matrix Multiply) - 双精度复数矩阵乘法

Matrix & Vector

• GeMV

  稠密矩阵 $\times$ 稠密向量

• SpMV (Sparse Matrix-Vector multiplication)

  稀疏矩阵 $\times$ 稠密向量

• SpMSpV（Sparse Matrix-Sparse Vector multiplication）

  稀疏矩阵 $\times$ 稀疏向量

Matrix & Matrix

• GeMM

  稠密矩阵 $\times$ 稠密矩阵

• SpMM (Sparse Matrix-Matrix multiplication)

  稀疏矩阵 $\times$ 稠密矩阵

• SpMSpM (Sparse Matrix Sparse Matrix multiplication)

  稀疏矩阵 $\times$ 稀疏矩阵

• SpGEMM (Sparse Generalized Matrix-Matrix multiplication)

  稀疏矩阵 $\times$ 稀疏矩阵

  相较于 SpMSpM，这里的 Generalized 表示该操作不仅限于常规数值乘法和加法，还可以自定义其他运算形式，覆盖更广泛的应用场景

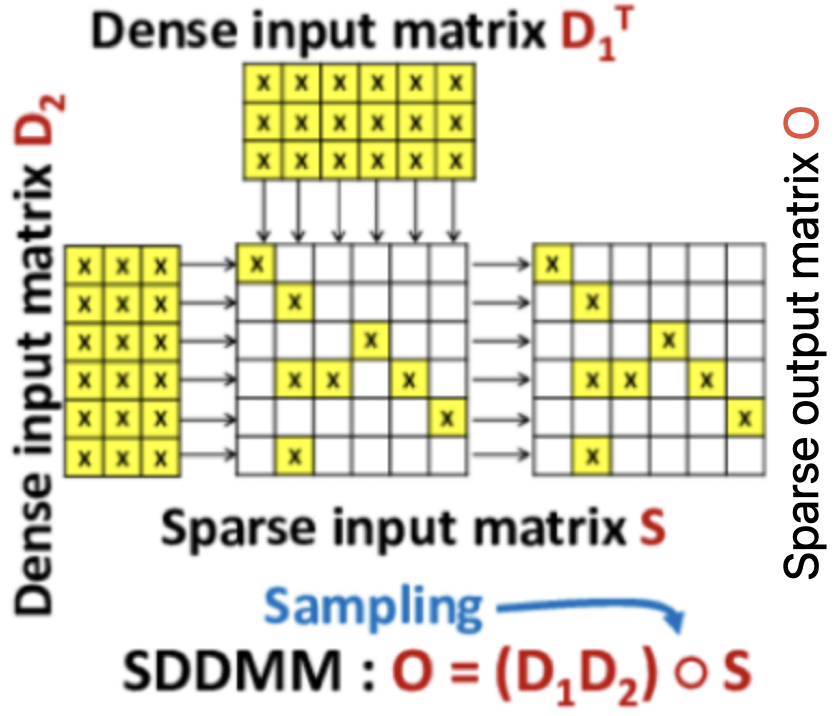
• SDDMM (Sampled-Dense-Dense Matrix Multiplication)

  稠密矩阵 $\times$ 稠密矩阵，最后经过一个稀疏矩阵的采样

  

Sparse Matrix Store Structure¹

1. CSR (Compressed Sparse Row) - 压缩稀疏行²

2. CSC (Compressed Sparse Column) - 压缩稀疏列
3. COO (Coordinate Format, also known as “ijv” or “triplet”) - 坐标格式
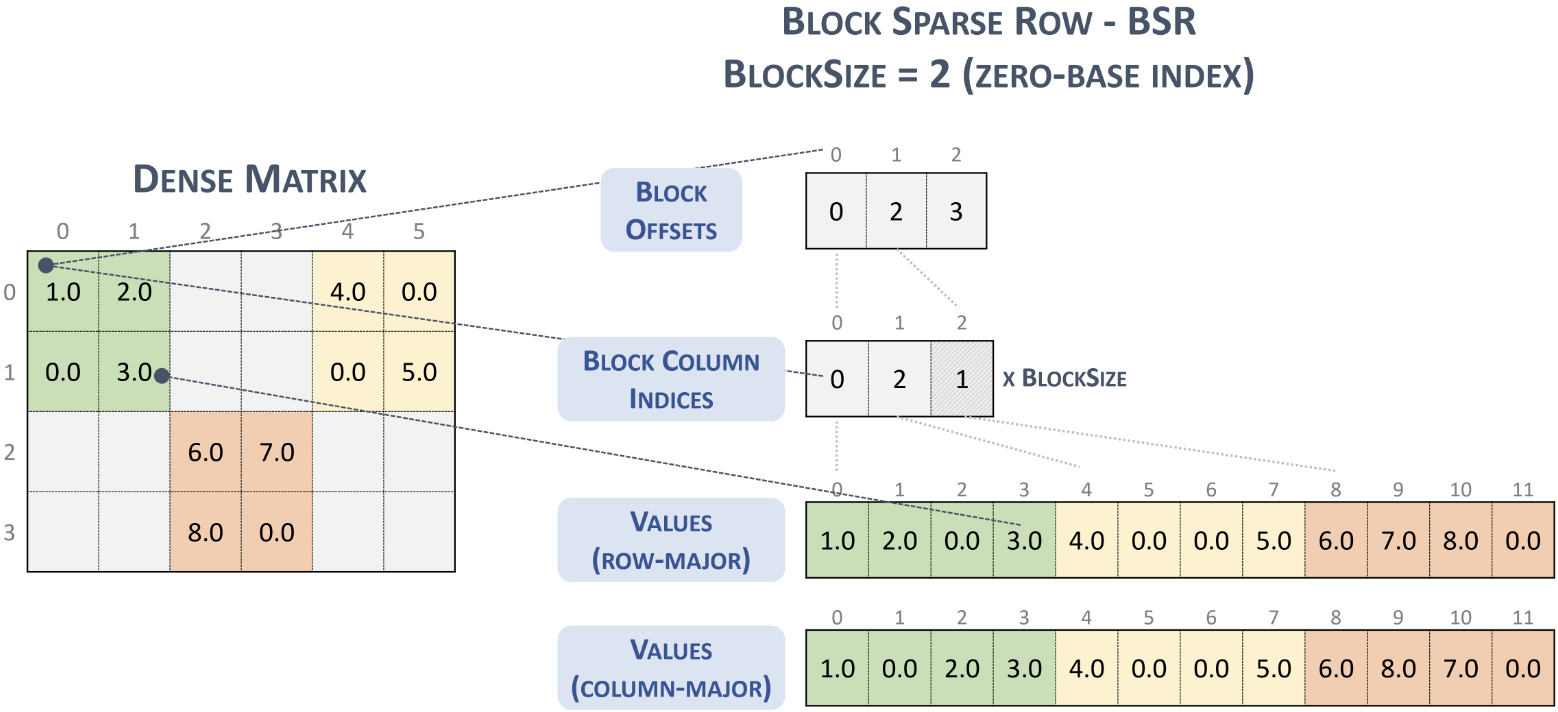
4. BSR (Block Compressed Sparse Row) - 块压缩稀疏行
5. ELL (Ellpack/Itpack format) - ELL压缩格式
6. DIA (Diagonal storage format) - 对角线存储格式
7. DOK (Dictionary of Keys) - 键字典格式

从 CSR 到 BSR，是对数据进行了分块，同时单位从每一个点转变为了每一块(所以实际就是以 CSR 结构存储了非零 block)，在组成上依然还是 row offset, col index 和 values 这 3 部分。

由于 block offsets 和 block column index 这两个字段的视角都是 block，所以对于每个 block 而言，目前是无法得知每个 block 内非零元的分布情况的，因此需要将零元和非零元均进行存储。

在稀疏矩阵下，每个 block 内部实际的非零元数量并不多，所以 values 字段的有效信息率是比较低的，因此就有了用二进制来优化存储的一些数据格式，用二进制标识非零元的数据分布情况，实际存储时只需要存储十六进制数，可以减少数据存储量，不过在实际运算时需要再转变为真实结构（简单来说就是时间换空间）。

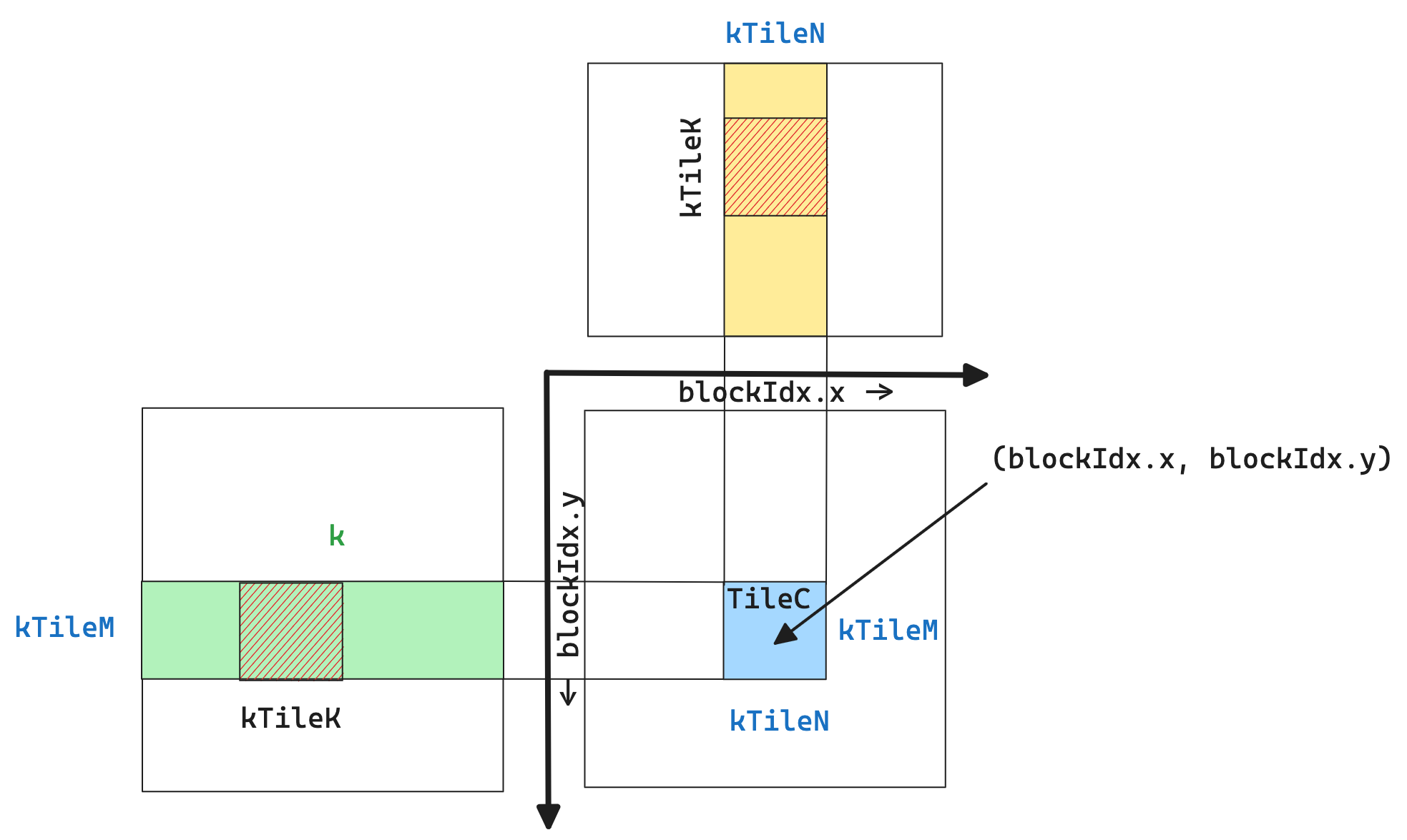
GEMM 任务划分策略

graph LR
    A[Sliced-K] --> B[Split-K]
    B --> C[Stream-K]

    %% 样式 - 可选，用于区分最终状态
    style A fill:#DCEFFB, stroke:#3A87AD
    style B fill:#DCEFFB, stroke:#3A87AD
    style C fill:#4CAF50, stroke:#2e7d32, stroke-width:3px, color:#FFFFFF

1. sliced-k

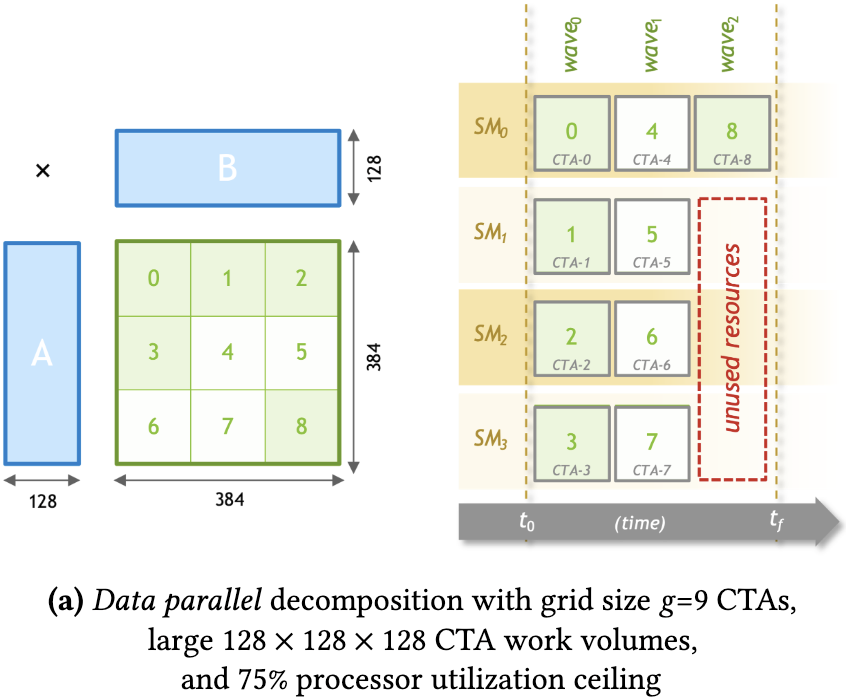
block 的数量和 M，N 维度相关，从 SM 使用率的角度来看，仅适用于 M，N 维度较大的情况

³

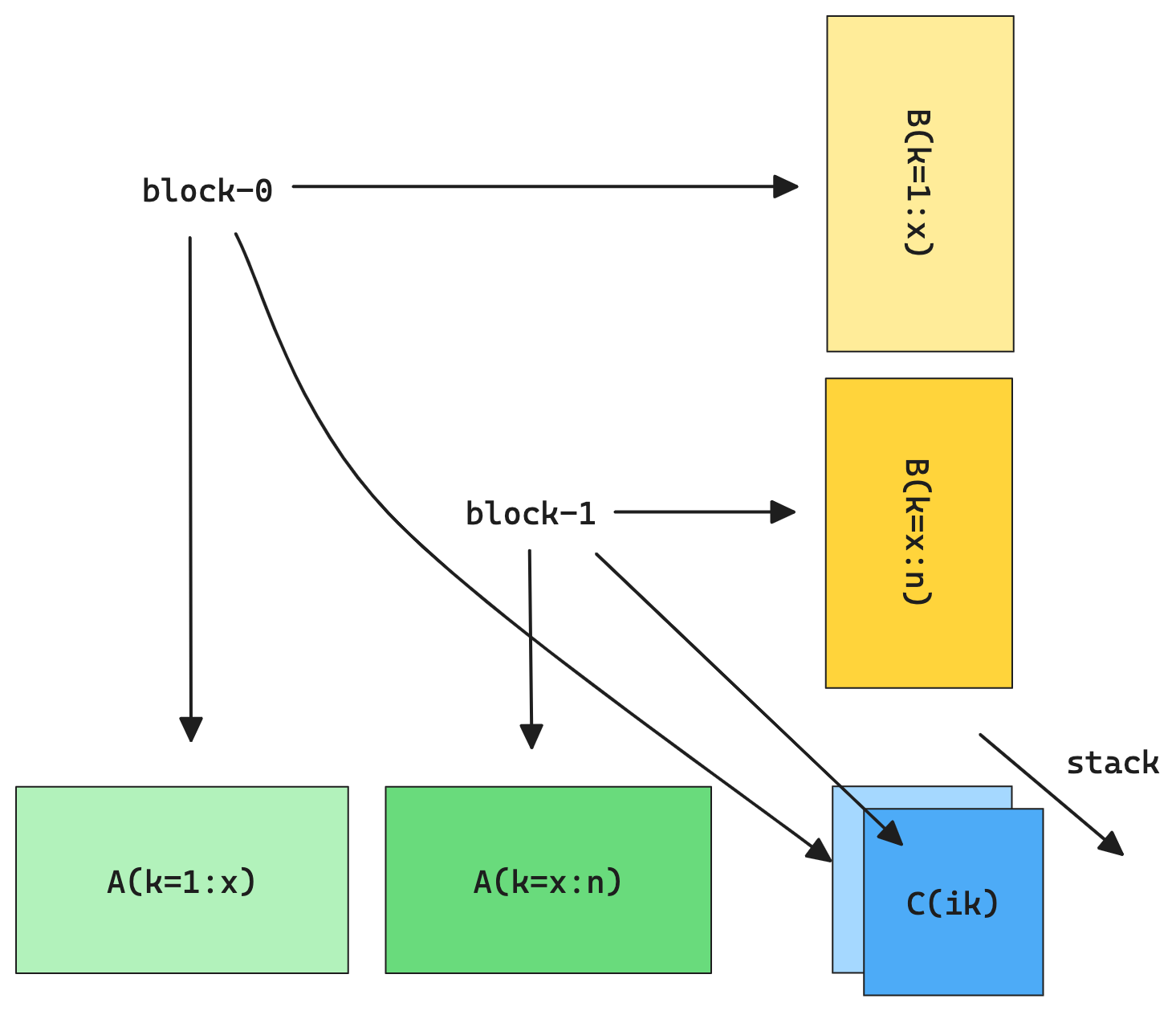
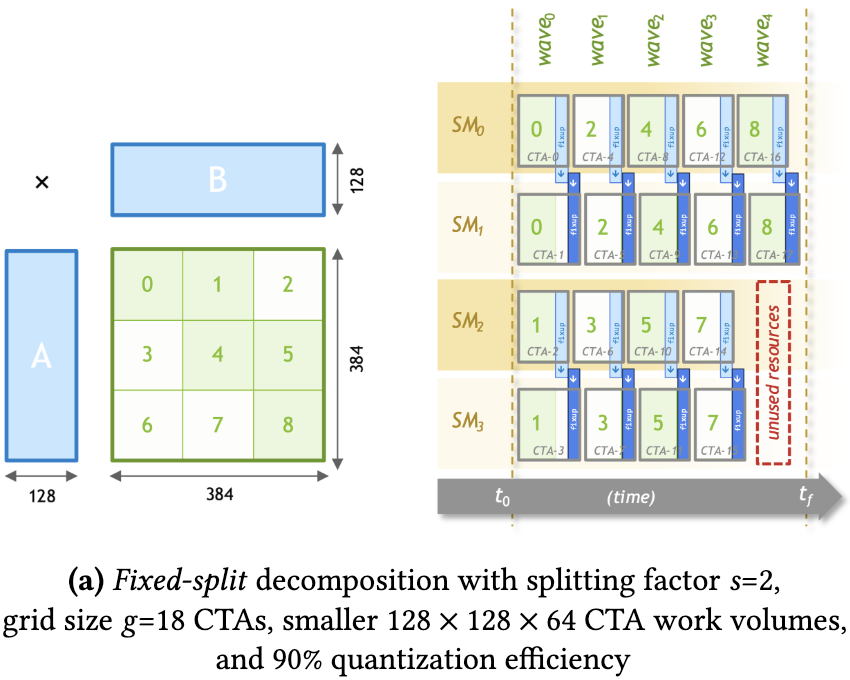
2. split-k

把 K 维度拆分给多个 block，但是最终涉及到结果汇总，存在写冲突问题

3. 静态划分任务方式的转换

对于前面提到的 sliced-k 和 split-k，在划分的任务数目和 SM 执行单元不能整除时，总会在存在某轮（wave）计算中存在 SM 空闲的问题

• sliced-k 情况：

⁴

• split-k 情况：

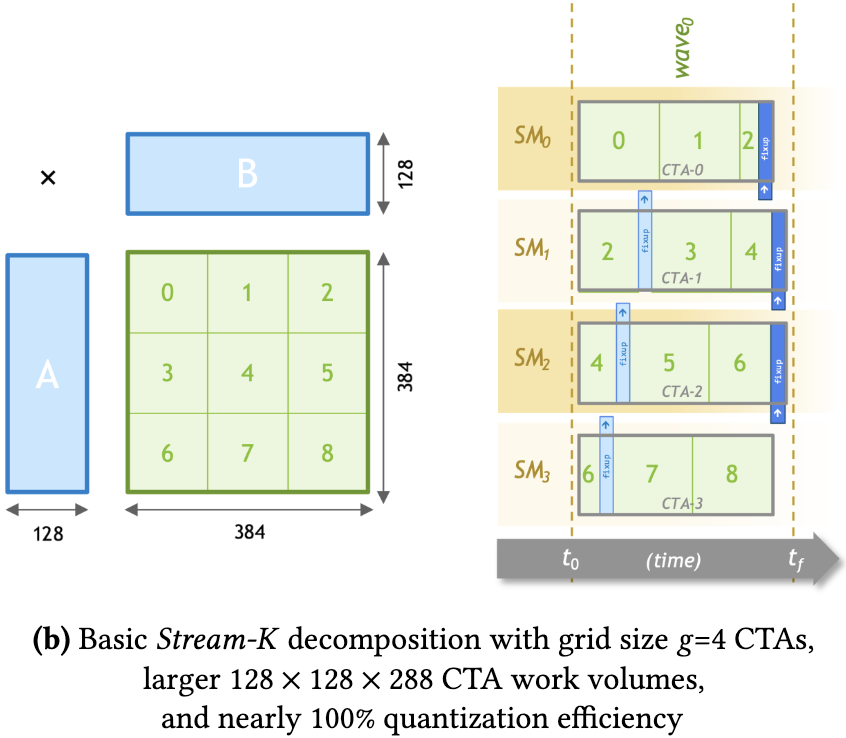
抛弃以任务为中心的划分逻辑，而是变成了以计算资源为核心的分配任务方式，使得SM的任务量基本相当，即 stream-k 方案

Stream-k: Work-centric parallel decomposition for dense matrix-matrix multiplication on the gpu

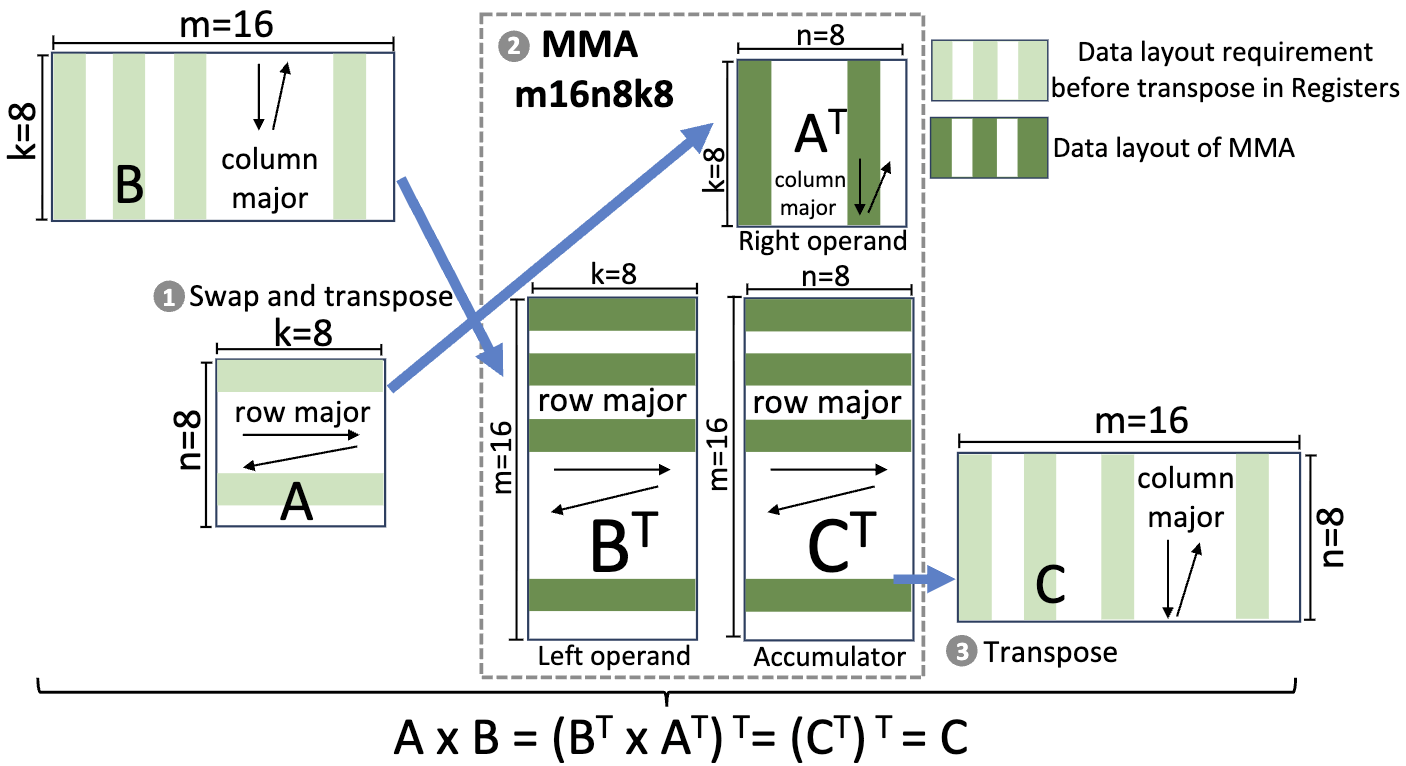
swap and transpose

⁵

需要额外说明的是寄存器行列主序的理解方式。通常认为寄存器只是存储变量的地方，没有主序之说。不过在 Tensor Core 的语境下，寄存器布局决定了数据在矩阵逻辑空间中的物理归属。这里所指的是指线程 ID 与矩阵坐标之间的映射关系。

• 行主序认为当线程号连续增加时，它们持有的寄存器分量在逻辑矩阵中是横向展开的
• 列主序认为当线程号连续增加时，它们持有的分量在逻辑矩阵中是纵向展开的

曾一度认为转置策略为 SpMM 所带来的收益源自于将稀疏矩阵 A 从左侧运算位移到右侧，消除了 16 这一个维度。但是分析 SDDMM 时发现

考虑为什么不同粒度下的零填充数量不同，从第一性原理的角度来说我们需要追本溯源，可以首先考虑整个过程是怎么发生的，具体而言就是零填充的过程是如何发生的。在这个过程中我们可以发现之所以需要进行零填充，关键就在于连续存储的方式，以 16x1 和 8x1 为例。那如果这种连续存储的需求或者情况不存在了，因为非连续情况就只存储非零即可，零填充数量随着粒度减少而减少的结论自然也就不存在了。当然这个和目前工作普遍采用的存储模式有关，现有工作都是先划分出 row windows，然后在 row window 内仅存储包含非零元的列，这种模式下行方向上就是连续的，列方向上就是离散的。

不过这种性质和结论一定程度上是来源于目前所采取的存储模式，或者说这些工作所提出的稀疏存储结构