SIMD Extension

Anonymous included in HPC
  

说明

SIMD Extension 的各种函数中参数的顺序以及各种函数的实现机制都是遵循着机器在实际存储时采用的小端序，注意在和数组混用时可能会产生一定思维上的混乱。

Categories

Hot to check the SIME extension support of cpu ?

1

cat /proc/cpuinfo
  1. For x86 instruction set
  • MMX
  • SSE (Streaming SIMD extensions)
  • AVX (Advanced Vector Extensions)
  • AVX2
  • AVX512

etc

  1. For ARM instruction set
  • NEON
  • AVX

Usage of SIMD intrinsic

header file

If you don’t know which header file to include, please find the function you want to call in Intel Intrinsics Guide，when you launch the detail of function, you will find the header file you need to include.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

<mmintrin.h>  MMX
<xmmintrin.h> SSE
<emmintrin.h> SSE2
<pmmintrin.h> SSE3
<tmmintrin.h> SSSE3
<smmintrin.h> SSE4.1
<nmmintrin.h> SSE4.2
<ammintrin.h> SSE4A
<wmmintrin.h> AES
<immintrin.h> AVX, AVX2, FMA

But there is a saying that

These days you should normally just include <immintrin.h>. It includes everything. 1

After actual testing(use SSE2 but include the <immintrin.h>), this statement has no problem.

compile option 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

-mmmx
-msse
-msse2
-msse3
-mssse3
-msse4.1
-msse4.2
-msse4
-mavx
-mavx2

You can search more compile options in gnu Option Summary | x86 Options.

Data load and store

The quantity of load and store function is limited. Taking functions for handling float date types as an example, there are only 4 most commonly used functions for loading and storing:

  1. __m256d _mm256_load_pd (double const * mem_addr)
  2. __m256d _mm256_loadu_pd (double const * mem_addr)
  3. void _mm256_store_pd (double * mem_addr, __m256d a)
  4. void _mm256_storeu_pd (double * mem_addr, __m256d a)

What we need to pay attention to is that what are the judgement strategy differences between aligned data and non aligned data when these functions executing.

About the knowledge of data align, you can reference this article, we will not talk it repeatly here.

Before we give the right answer of this question, we can see some code snippets

This is a plain version of $ x = a \times x $ implementation.

1
2
3
4
5
6
7

void sapxy(int n, float a, float *x)
{
  int i;
  for (i=0; i<n; i++) {
    x[i] = x[i] * a;
  }
}

We can use SIMD extension to optimize the above code.

  • If we use the first line sse_sapxy function call, we will get “Segmentation fault (core dumped)”.
  • If we use the second line code, we will get the right result.
  • If we use the third line code, we will get the wrong result but we will not get the “Segmentation fault (core dumped)”.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

void sse_sapxy(int n, float a, float *x)
{
  float aa[4];
  aa[0] = aa[1] = aa[2] = aa[3] = a;

  __m128 v_a = _mm_load_ps(aa);

  int i;
  for (i = 0; i < n / 4 * 4; i += 4) {
    __m128 v_x = _mm_load_ps(x + i);
    v_x = _mm_mul_ps(v_x, v_a);
    _mm_store_ps(x + i, v_x);
  }

  for (; i < n; i++) {
    x[i] = x[i] * a;
  }
}

float a[1000000];

int main() {
  for (int i = 0; i < 1000000; i++) {
    a[i] = i * 1.0;
  }

  sse_sapxy(999999, 3.14159, a + 1);
  // sse_sapxy(1000000, 3.14159, a);
  // sse_sapxy(999996, 3.14159, a + 4);
}

Now, let’s see the right implementation of SIMD extension optimize version code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

void sse_sapxy_unaligned_load(int n, float a, float *x)
{
  float aa[4];
  aa[0] = aa[1] = aa[2] = aa[3] = a;
  
  __m128 v_a = _mm_loadu_ps(aa);

  int i;
  if (((unsigned long long)x % 16) == 0) { // check if memory is aligned.
    for (i = 0; i < n / 4 * 4; i += 4) {
      __m128 v_x = _mm_load_ps(x + i);
      v_x = _mm_mul_ps(v_x, v_a);
      _mm_store_ps(x + i, v_x);
    }
  } else {
    for (i = 0; i < n / 4 * 4; i += 4) { 
      __m128 v_i = _mm_loadu_ps(x + i);
      __m128 v_o = _mm_mul_ps(v_i, v_a);
      _mm_storeu_ps(x + i, v_o);
    }
  }

  for ( ; i < n; i++)
    x[i] = a * x[i];
}

Why we get the above result, the reason is that b and b + 4 is satisfied with the data aligned requirement of _mm_load_ps and _mm_store_ps, but b + 1 isn’t satisfied with it, so we should use right load and store function for one data.

simd extension 提供给用户的就是这么一条指令，但是在底层执行时，如果是确定地址对齐的数据，在load时只需要进行一次内存访问，就可以将所有数据加载到 vector register 中了。

但是如果地址不对齐的数据，这部分数据是可能跨越memory page 的，那么底层在执行时，对于这部分数据的访问就可能需要多次内存访问，最终需要将多次内存访问读取到的数据都合并到一个 vector register 中，合并数据是需要额外的操作逻辑的，所以这里又提供了一个新的函数单独做非对齐数据的加载。

实际上，从一个库的实现角度来说，这里有两种实现思路，一种是封装层次更高的，即只给上层用户提供一个简单的load函数，由函数实现本身来区分数据是否对齐，另一种就是目前的由用户来显式指定，之所以采用后者，我觉得可能是因为这些函数本身就是比较底层的概念了，没必要实现太高层次的封装，级别更高层次的封装往往都是框架来做的。

At last, we can see a further optimized version, when judge the aligned data, this code uses the pointer directly, save the data copy time from memory to vector register.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

void sse_sapxy_unaligned(int n, float a, float *x)
{
  float aa[4];
  aa[0] = aa[1] = aa[2] = aa[3] = a;
  
  __m128 v_a = _mm_loadu_ps(aa);

  int i;
  if (((unsigned long long)x % 16) == 0) { // check if memory is aligned.
    __m128 *p = (__m128 *)x;
    for (i = 0; i < n / 4 * 4; i += 4) {
      *p = _mm_mul_ps(*p, v_a);
      p++;
    }
  } else {
    for (i = 0; i < n / 4 * 4; i += 4) { 
      __m128 v_i = _mm_loadu_ps(x + i);
      __m128 v_o = _mm_mul_ps(v_i, v_a);
      _mm_storeu_ps(x+i, v_o);
    }
  }

  for ( ; i < n; i++)
    x[i] = a * x[i];
}

Data process

Vector Addition 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

// compile with -mavx

#include <immintrin.h>
#include <iostream>

int main() {
    double a[] = {1.0 , 2.0, 3.0, 4.0};
    double b[] = {4.0, 3.0, 2.0, 1.0};
    double dst[4];

    __m256d va = _mm256_loadu_pd(a);
    __m256d vb = _mm256_loadu_pd(b);

    __m256d vdst = _mm256_add_pd(va, vb);

    _mm256_storeu_pd(dst, vdst);

    for (int i = 0; i < 4; i++) {
        std::cout << dst[i] << ' ';
    }
    std::cout << std::endl;

    return 0;
}

Horizontal Addition

The effect of this function is confusing, because it store the two array’s adjacent data sum crossly. I can not image the usage in realistic scenes.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

#include <immintrin.h>
#include <iostream>

int main() {
    double a[] = {1.0, 1.0, 2.0, 2.0};
    double b[] = {3.0, 3.0, 4.0, 4.0};
    double hsum[4];

    __m256d va = _mm256_loadu_pd(a);
    __m256d vb = _mm256_loadu_pd(b);
    __m256d vhsum = _mm256_hadd_pd(va, vb);

    _mm256_storeu_pd(hsum, vhsum);

    for (int i = 0; i < 4; i++) {
        std::cout << hsum[i] << ' ';
    }
    std::cout << std::endl;

    return 0;
}

The result of the above code is

2 6 4 8

Compare

__m256d _mm256_cmp_pd (__m256d a, __m256d b, const int imm8)

According to the third parameter to compare the data from first and second vector, and output the result to a __m256d vector.

The third parameter value and its corresponding meaning are shown in the table below.

imm8[4:0]操作符含义
0_CMP_EQ_OQ比较两个操作数是否相等（Ordered, Quiet）
1_CMP_LT_OS比较第一个操作数是否小于第二个操作数（Ordered, Signaling）
2_CMP_LE_OS比较第一个操作数是否小于等于第二个操作数（Ordered, Signaling）
3_CMP_UNORD_Q比较两个操作数是否未排序（Unordered, Quiet）
4_CMP_NEQ_UQ比较两个操作数是否不相等（Unordered, Quiet）
5_CMP_NLT_US比较第一个操作数是否不小于第二个操作数（Unordered, Signaling）
6_CMP_NLE_US比较第一个操作数是否不小于等于第二个操作数（Unordered, Signaling）
7_CMP_ORD_Q比较两个操作数是否有序（Ordered, Quiet）
8_CMP_EQ_UQ比较两个操作数是否相等（Unordered, Quiet）
9_CMP_NGE_US比较第一个操作数是否不大于等于第二个操作数（Unordered, Signaling）
10_CMP_NGT_US比较第一个操作数是否不大于第二个操作数（Unordered, Signaling）
11_CMP_FALSE_OQ始终返回假（Ordered, Quiet）
12_CMP_NEQ_OQ比较两个操作数是否不相等（Ordered, Quiet）
13_CMP_GE_OS比较第一个操作数是否大于等于第二个操作数（Ordered, Signaling）
14_CMP_GT_OS比较第一个操作数是否大于第二个操作数（Ordered, Signaling）
15_CMP_TRUE_UQ始终返回真（Unordered, Quiet）
16_CMP_EQ_OS比较两个操作数是否相等（Ordered, Signaling）
17_CMP_LT_OQ比较第一个操作数是否小于第二个操作数（Ordered, Quiet）
18_CMP_LE_OQ比较第一个操作数是否小于等于第二个操作数（Ordered, Quiet）
19_CMP_UNORD_S比较两个操作数是否未排序（Unordered, Signaling）
20_CMP_NEQ_US比较两个操作数是否不相等（Unordered, Signaling）
21_CMP_NLT_UQ比较第一个操作数是否不小于第二个操作数（Unordered, Quiet）
22_CMP_NLE_UQ比较第一个操作数是否不小于等于第二个操作数（Unordered, Quiet）
23_CMP_ORD_S比较两个操作数是否有序（Ordered, Signaling）
24_CMP_EQ_US比较两个操作数是否相等（Unordered, Signaling）
25_CMP_NGE_UQ比较第一个操作数是否不大于等于第二个操作数（Unordered, Quiet）
26_CMP_NGT_UQ比较第一个操作数是否不大于第二个操作数（Unordered, Quiet）
27_CMP_FALSE_OS始终返回假（Ordered, Signaling）
28_CMP_NEQ_OS比较两个操作数是否不相等（Ordered, Signaling）
29_CMP_GE_OQ比较第一个操作数是否大于等于第二个操作数（Ordered, Quiet）
30_CMP_GT_OQ比较第一个操作数是否大于第二个操作数（Ordered, Quiet）
31_CMP_TRUE_US始终返回真（Unordered, Signaling）

set

__m256d _mm256_set_pd (double e3, double e2, double e1, double e0)

This funciont doesn’t have any special effect, it just set value for a vector register. What we need to pay attention to is that the order of the parameters of this function.

The order of this function follows the real store order of machine, i.e. little-endian（小端序，低有效字节存储在低位，最右侧的位置就是低有效字节以及低位，所以所这种布局遵循了机器的小端序）

insert

insert a __m128d vector data into __m256d vector data.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <immintrin.h>
#include <iostream>

int main() {
    double a[] = {1.0 , 2.0, 3.0, 4.0};
    double b[2] = {5.0, 6.0};
    double dst0[4], dst1[4];

    __m256d va = _mm256_loadu_pd(a);
    __m128d vb = _mm_loadu_pd(b);

    __m256d vdst0 = _mm256_insertf128_pd(va, vb, 0);
    __m256d vdst1 = _mm256_insertf128_pd(va, vb, 1);

    _mm256_storeu_pd(dst0, vdst0);
    _mm256_storeu_pd(dst1, vdst1);

    std::cout << "dst0: ";
    for (int i = 0; i < 4; i++) {
        std::cout << dst0[i] << ' ';
    }
    std::cout << std::endl;

    std::cout << "dst1: ";
    for (int i = 0; i < 4; i++) {
        std::cout << dst1[i] << ' ';
    }
    std::cout << std::endl;

    return 0;
}

The result of the above program is that

dst0: 5 6 3 4

dst1: 1 2 5 6

Permute

__m256d _mm256_permute4x64_pd (__m256d a, const int imm8)

According to the imm8 to select the data in a and put it into a __m256d vector register.

What we should pay attention to is that imm8 is a hexadecimal data, for example, if we want to express 11111111, we should use the 0xFF.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

#include <immintrin.h>
#include <iostream>

int main() {
    double a[] = {1.0 , 2.0, 3.0, 4.0};
    double dst[4];

    __m256d va = _mm256_loadu_pd(a);
    __m256d vdst = _mm256_permute4x64_pd(va, 0xE4);

    _mm256_storeu_pd(dst, vdst);

    for (int i = 0; i < 4; i++) {
        std::cout << dst[i] << ' ';
    }
    std::cout << std::endl;

    return 0;
}

0xE4 is 11100100, i.e. it corresponding to the order of array a. So the result is

1 2 3 4

blend

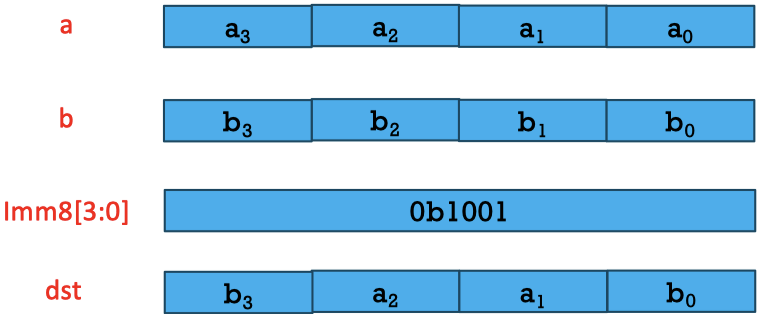
https://cdn.jsdelivr.net/gh/gaohongy/cloudImages@master/202406041036210.png

Traverse the imm from the LSB to HSB, if the bit value is 1, select b data and put it into the result vector resigter, other wise select a data.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

#include <immintrin.h>
#include <iostream>

int main() {
    double a[] = {1.0 , 2.0, 3.0, 4.0};
    double b[] = {5.0, 6.0, 7.0, 8.0};
    double dst[4];

    __m256d va = _mm256_loadu_pd(a);
    __m256d vb = _mm256_loadu_pd(b);

    __m256d vdst = _mm256_blend_pd(va, vb, 0xA); // 0xA: 1010

    _mm256_storeu_pd(dst, vdst);

    for (int i = 0; i < 4; i++) {
        std::cout << dst[i] << ' ';
    }
    std::cout << std::endl;

    return 0;
}

1010 is mapping to the baba, so when we output the dst data from low byte to high byte, we will get the “a b a b”, i.e. the result of this program is “1 6 3 8”.

broadcast 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

#include <immintrin.h>
#include <iostream>

int main() {
    double a2[] = {1.0, 2.0};
    double a4[4];

    __m128d va2 = _mm_loadu_pd(a2);

    __m256d va4 = _mm256_broadcast_pd(&va2);

    _mm256_storeu_pd(a4, va4);

    for (int i = 0; i < 4; i++) {
        std::cout << a4[i] << ' ';
    }
    std::cout << std::endl;

    return 0;
}

The result is

1 2 1 2

  1. Header files for x86 SIMD intrinsics ↩︎

Updated on 2024-06-05 
Back | Home
0%